どうもメガネです。
この前インダクタの設計に関する問題でちょっと面白いなぁと思ったことがあったので
まとめておきます。
磁束密度Bと断面積Sと磁束φの関係
磁束密度Bと磁束が鎖交、貫通する面の断面積S、磁束の大きさφは以下の関係式で与えられます。
有名な式ですね。
$$\phi=BS$$
これを磁束密度$B$を求める形にすれば、
$$B= \frac{\phi}{S}$$
この式を見れば、どう考えても断面積$S$を大きくすれば磁束密度&B&は小さくなりそうですよね。
ただそうもいかんことがあるという、そういう話です。
インダクタの場合で考える
今回はインダクタ、それも巻き線が二つあるような2巻き線インダクタを考えます。
まぁ、変圧器といってもいいかもしれませんが。
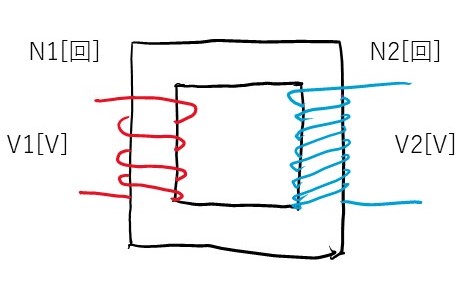
に巻き線インダクタのフリー画像とかマニアックすぎてなかったですね。
まぁ、それは置いておくとして、、、
一次側、もしくは二次側のコイルが発生する磁束$\phi$はそのコイルに流れている電流$i$と磁気抵抗$R$を用いて以下の式で与えられます。
$$\phi= \frac{N i}{R}$$
つまりインダクタに発生する全磁束$\phi$は、磁気抵抗$R$は共通のものとして使えるので、
$$\phi= \frac{N_1 i_1}{R}+ \frac{N_2 i_2}{R}$$
と表されるわけですねぇ。
でーは、では、磁気抵抗$R$はどういう式で表されるかというと、
コアの磁路長$l_i$と真空中の透磁率$\mu_0$、コアの材料による比透磁率$\mu_r$、コアの断面積$S$を使って、
$$R=\frac{l_i}{\mu_0\mu_r \ S} $$
と表されます。
いまコアにギャップ(空隙)があるなら、ギャップ長を$l_g$として、
$$R=\frac{l_i}{\mu_0\mu_r \ S}+ \frac{l_g}{\mu_0\ S} $$
と表されます。
ではでは、いままで出てきた式を使ってまとめてみます。
電流は大文字のIにします。
$$B=\frac{\phi}{S}$$
$$= \frac{1}{S} \left( \frac{N_1 I_1}{R}+ \frac{N_2 I_2}{R} \right) $$
$$=\frac{1}{S} \frac{1}{R}(N_1I_1+N_2I_2)$$
$$=\frac{1}{S} \frac{1}{ \left(\frac{l_i}{\mu_0 \mu_r S}+ \frac{l_g}{\mu_0 S} \right) } (N_1I_1+N_2I_2) $$
ここで$\frac{1}{S}$を外側にくくりだしてやると、
$$=\frac{1}{S} \frac{1}{ \frac{1}{S} \left(\frac{l_i}{\mu_0\mu_r}+ \frac{l_g}{\mu_0} \right) } (N_1I_1+N_2I_2) $$
おっとぉ、分子と分母に同じものがありますねぇ、、、
消してやると、
$$= \frac{1}{\left(\frac{l_i}{\mu_0\mu_r}+ \frac{l_g}{\mu_0} \right) } (N_1I_1+N_2I_2) $$
となりますねぇ。
つまり、2巻線のインダクタ(変圧器)を設計するときには、磁束密度B、鎖交磁束φ、鎖交断面積Sが
$$B=\frac{\phi}{S}$$
で表されるにも関わらず、
上の式を分解・展開していくと断面積$S$がなくなってしまうんですねぇ。
これは驚きだぁw。
つまり、断面積$S$を大きくしても、磁束密度$B$は下がらんというわけですね。
無論、今のようにインダクタを考えて磁気抵抗$R$を考えているときによりますが。
定義式ではSを減らせばBが減るのは当たり前ですからね。
まとめ
以上、インダクタの設計において、φ=BSが成り立たんぞ、ということをやってみました。
電気の界隈ではφ=BSと言えば不変の式だとはおもいますが、設計する内容によってこうも変わってしまうんですねぇ、、、
面白い問題だなぁと思ったのでまとめてみました。
また、気になるようなものがあったら載せてみようと思います。
読んでいただきありがとうございました。
