どうもメガネです。
今日はボード線図の書き方を載せてみたいと思います。
ボード線図は制御工学に一度でも触れれば必ず勉強するものですが、結構「書く」となると、
案外コンピュータ任せなのが実態なようで、テストとかで手書きで書かされるとなると以外に書き方が分からなくなったりします。
今回は描き方を簡単に紹介します。
ネットにあんまり載ってない
まずは余談から。
んん~、、ネットで「ボード線図 描き方」でググると大量に記事が出てくるんだけど、
これがあんまり使えないんですよね。
記事数自体はだいぶ乗ってはいるんですが、中身を除いていみると、
「位相特性とゲイン特性の周波数依存特性を読み取ることができます!」みたいな単なる紹介だったり、
「エクセルで作成します」とか「電卓で計算していくとかけます!」とかがいっぱい、、
いや、ね。わかるんだけど、テスト前の俺は単なる書き方が知りたいんだぁ!!!!!!
って人にはちょっと無意味な情報になっちゃったりします。
まぁ、つまるところ、
そうじゃねえよ。俺は単に簡単に手で描く方法が知りたいんだよ。
という私の求める答えはあるように見えてなかったです。
もちろん意味を考えて描くことも大事ですが、まずはかけないとそもそも話にならないと思うので、今回は「機械的に」これをやればかけるよ。という方法を紹介していきたいと思います。
今回考える伝達関数
今回はかなり簡単な伝達関数を例に考えてみます。
メジャーな以下の一次遅れ伝達関数を考えてみることにしましょう。
$\displaystyle G(s)= \frac{1}{1+Ts}$
周波数特性を考える時は$s$に$j\omega$を代入するんでしたね。
あと周波数特性を考える時は、$j\omega$を代入した$G(s)$を$F(s)$とおいて考えることが多いです。
Fは周波数(frequency)のFだったはずです。
結構こういう勝手な置き換えが途中で行われるとめんどくさいですよねぇ、、、
ゲイン特性を書く
まずはゲイン特性を考えてみます。
ゲイン特性は以下の式で定義されています。
$\displaystyle g=20log_{10}(|F(j\omega)|)$
これについて、今回の計算の場合を考えてみます。
まず一次遅れ系の伝達関数のノルム(大きさのこと)をとってみます。
$\displaystyle |F(j\omega)|=\frac{1}{\sqrt{1^2+{(\omega T)}^2}}$
いったん分子に$j$を持って行ってから計算してもいいですが、分子が1の時は分母で大きさをとってしまってから考えてもいいですね。
これを先ほどのゲインの定義式に代入します。分数を$X^{-1}$の表記で代入すると、
$\displaystyle g=20log_{10}(|F(j\omega)| $
$\displaystyle g=20log_{10} \left( \frac{1}{\sqrt{1^2+{(\omega T)}^2}}\right)$
マイナスが前に出てきます。
$\displaystyle g=-20log_{10} \sqrt{1^2+{(\omega T)}^2}$
これでゲイン特性の式は導出できました。
これをもとに考えてみます。
最初に一度解答をのせてみる
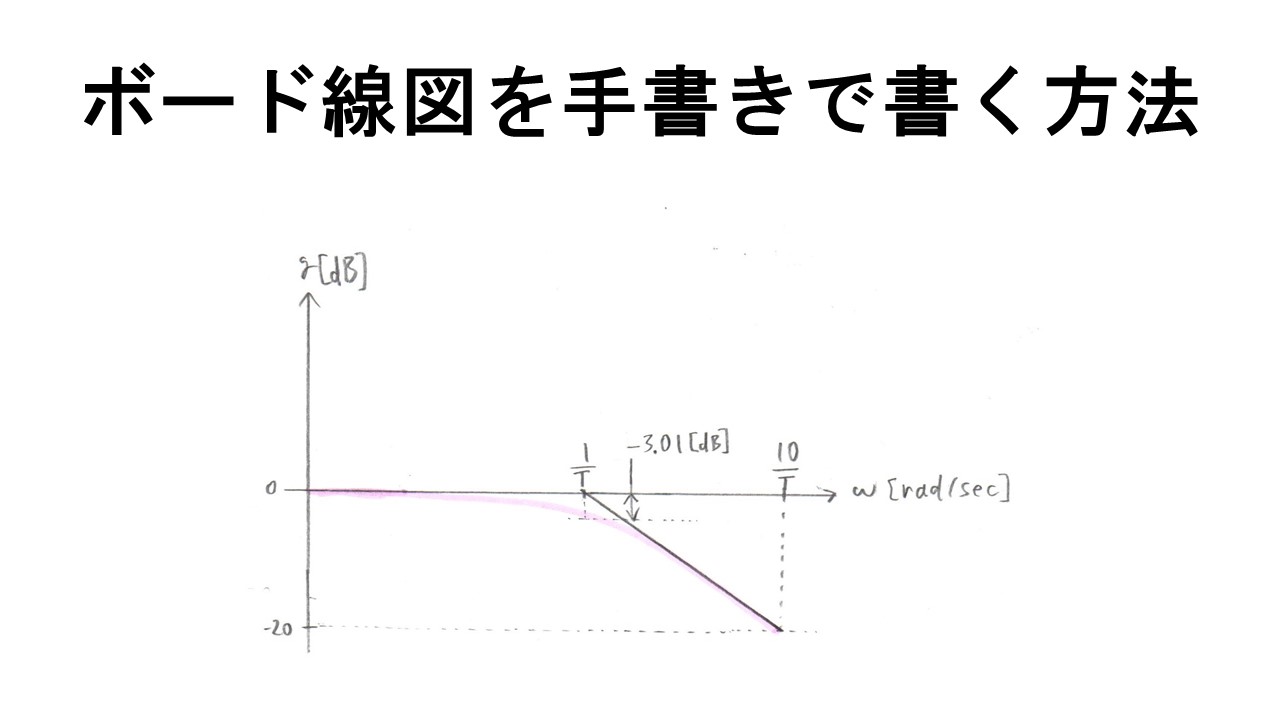
まずは解説しやすいように最初に答えを述べると、この一次遅れ系のゲイン特性曲線は以下のような形になります。

この図での黒線($\frac{1}{T}$まで0でそこから-20度まで下がる線)が一般的な問題とかで描かされる
近似したゲイン特性曲線になります。
赤のマーカーで書いたものが、
実際の特性曲線になります。(電卓とかで計算してできるやつ)
そして忘れないでいてほしいのですが、横軸は対数で書かれています。(片対数というやつ)
なので周波数は1倍、10倍、100倍、、という広い範囲でのゲイン特性を見ることができます。
たいていの場合、ボード線図の概形を書かせる問題では近似した直線型のものを書かせるものがほとんどだと思います。
これの書き方について考えます。
式を観察してみる
ゲイン特性曲線は、「グラフが変化する点」が分かればあとは点と点を結ぶだけです。
なので変化するところを考えてみます。
まず先ほど導出した以下の式をよく見てみます。
$\displaystyle g=-20log_{10} \sqrt{1^2+{(\omega T)}^2}$
$log$関数は中身が増えれば関数全体も増えるのはイメージできますね。ただし$-20$というマイナスの符号付きであるので、$log$の中身の$\omega$が増えれば負の方向に増えそうな感じがします。
$\displaystyle g=-20f(x)$
って考えればイメージできますね。
ここで$\omega$が$\frac{1}{T}$の時を考えてみます。
導出した式に代入すると、
$\displaystyle g=-20log_{10} \sqrt{1^2+{(\frac{1}{T} T)}^2}$
$\displaystyle g=-20log_{10} \sqrt{2}$
となります。
実はこれが特徴的な点で、折点角周波数、などと呼ばれたりもしますが、ここでゲイン特性の曲線が折れます。
この式になるとき、つまり今回なら$\omega$が$\frac{1}{T}$になるときに折れる、と覚えておけばいいわけです。
一般化して考えるなら、 $\displaystyle g=-20log_{10} \sqrt{2}$ の形になる$\omega$で折れる、といってもいいかもしれません。
別に$log$の中身を計算するわけではないので、これを覚えておけば変化点の一つ目はかけます。
グラフの変化の仕方を大まかに予想する方法ですが、たいていの場合は$A+jB\omega$みたいな形になるので、大抵$log_{10}$のうしろは$sqrt{A^2+(B\omega)^2}$の形になるので、ほかの場合にも適用できます。
※ちなみにですが、電卓で正確に計算を行ってみると、
$\displaystyle g=-20log_{10} \sqrt{2}=-3.010...[dB]$
となります。
これは$\omega=\frac{1}{T}$において赤のマーカでかいたグラフの方で、この時実際のゲインと近似曲線によるゲインとの差が最大になります。
$\frac{1}{T}$以降の形はどうなるのか
先ほどまでの説明で、ゲイン特性が最初に変化する(折れ始める)場所を求めることができました。
今度はそれ以降で変化する場所を考えてみます。
もう一度導出したゲインの式を出します。
$\displaystyle g=-20log_{10} \sqrt{1^2+{(\omega T)}^2}$
ここで$\omega$が1に比べて非常に大きい時を考えてみます。その場合近似して以下のように式を変形できます。
$\displaystyle g=-20log_{10} \sqrt{1^2+{(\omega T)}^2}$
$\displaystyle g \simeq -20log_{10} \sqrt{(\omega T)^2}$
$\displaystyle g =-20log_{10} \omega T$
これで変形ができました。
教科書によってはここからさらに$log$の中身を引き算の形にするのがあるのですが、個人的にはかえって意味が分からなくなる気がするのでここで変形は終えておきます。
この式の意味を考えてみると、まず$T$は与えられた伝達関数の定数なので、変化するのは$\omega$だけです。
よって、$\omega$が増えるとgはマイナスの方向に増えていきそうな感じがイメージできます。
実際どんな形になるのかこの形からは少し想像しにくい感じがしますが、答えから言うと、
今底が10の$log$を考えているので、$log$の中身が10倍、100倍、、、と増えていけば、
横軸を対数に撮った場合(10倍、100倍、、を等間隔で取った場合)、グラフは直線になります。
傾きは負なので下方向に直線で伸びるグラフ、になりそうですね。
ただまぁ、直線になるといってもどうやって書けばわからんので、ここは実際に値を代入してみます。
もちろん電卓はいらないです。
底が10なので、10のn乗の数を入れるときれいに出ます。なぜなら、
$\displaystyle log_{10} 10=1$ときれいにまとめられるからです。
今回は$log$の中身にTという邪魔なものがあるので、これを消すために$\frac{1}{T}$したもの、つまり
$\frac{10}{T}$を代入してみることにします。すると、
$\displaystyle g =-20log_{10} \frac{10}{T} T=-20\times 1=-20$
つまり、$\omega=\frac{10}{T}$で-20[dB]になる、というわけです。
これで二点目が分かってしまったわけです。
あとは結ぶだけですねぇ。
ここまでの内容をまとめる
今回の一次遅れ系について、今までに求めたものをまとめてみると以下のようになります。
①ゲイン特性曲線は$\frac{1}{T}$で変化を始める。
②$\omega$が大きい時は、ゲインは直線でマイナス方向に変化する。
③$\omega=/frac{10}{T}$におけるゲインは-20[dB]になる
こんな感じです。
なんとなくかけそうですね。
③に関しては別にきれいに(電卓を使わなくても)まとまれば、-20[dB]でなくても大丈夫です。
あくまで①と③で求めた点が結びつくことを知っていればいいわけです。
ただまだ近似において少しあいまいな部分があるのでここで近似における条件をまとめておきます。
①ゲインが-3.01[dB]になるまでの区間は、近似では0にして大丈夫
つまり$-20log_{10} \sqrt{2}$となる$\omega=\frac{1}{T}$まではずっとゲインは0で描くということです。
$\omega=\frac{1}{T}$以降は直線で変化するとみなす
つまり、$\omega=\frac{1}{T}$以降は直線で変化するとみなし、それ以降の点と結んでいいということです。
つまり、$\omega= \frac{1}{T}$、$g=0$と、$\omega=\frac{10}{T}$、$g=-20$を直線で結んでいいということです。
一点だけじゃ心配だなぁ~という人は、$\frac{100}{T}$などを代入してみてもいいですね。
実際には-3.01[dB]の誤差が出るんですが、手書きで書く場合はこれは無視することが多いようです。
これを実際にやると、以下のようなゲイン特性曲線が描けるわけです。
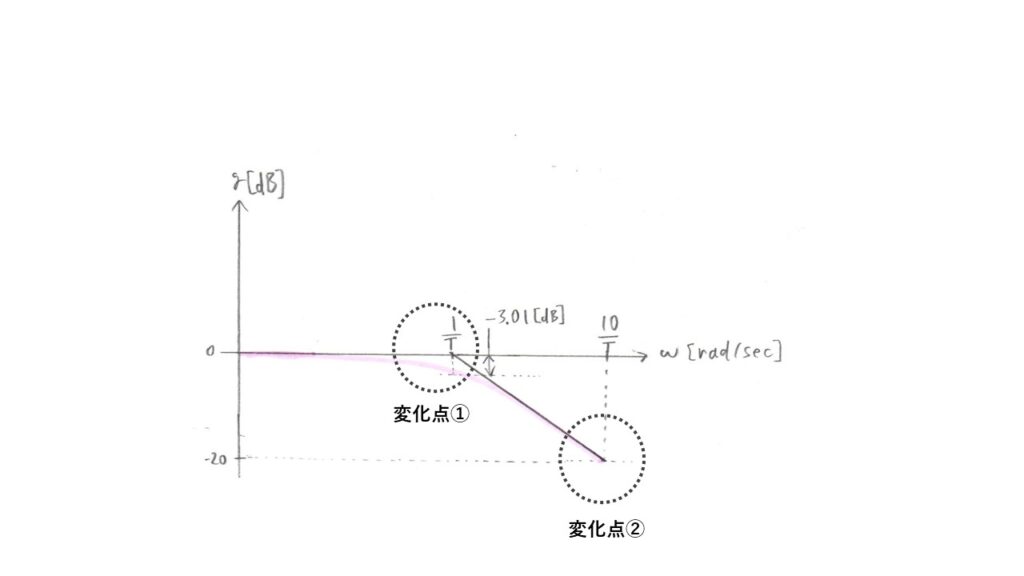
近似の程度によって書き方は変わると思いますが、制御の教科書や参考書などを見た感じ大抵この方法で近似していたので問題ないと思います。
ただし次数が高い伝達関数の場合は変化点が何度も現れることがあるので、どことどこの変化点を無図ぶべきかは確認しましょう。
まとめ
今回はゲイン特性曲線のかきかたについて、近似まで方法を端折らずに書いてみました。
ちょっとくどいですが機械的に描く手順のようなものがあまり見られなかったのまとめてみました。
あとで位相特性曲線の方もまとめてみようと思います。
それでは。