この記事では「LPFの離散化方法」、「意味」、「実際のプログラム」について一例を紹介しています。
今回はローパスフィルタを離散系に直すという処理について、自分なりにまとめて置こうと思います。
実際の手順は簡単なんですが、いざやろうとなると「じゃあ実際どうやったらいいの?」という感じで手が止まることが以外に多いと思ったので備忘録的にまとめておきます。
この技術と知識の微妙な壁、ないようでありますよねぇ。。。
ローパスフィルタ(LPF)を離散系に直したい
ローパスフィルタ。
ノイズ防止や値の整備、その他もろもろ、多分一番よくつかわれるフィルターなんじゃないかと思います。
アナログ回路に使用されるローパスフィルタであれば、信号ラインに直列に抵抗を、並列にキャパシタを接続すれば完成です。
ですが離散系、マイコン内の処理で使用するとなると、どうやってプログラムに落とし込めばよいのだろう?ってなりますよね。
少なくとも自分は最初そう思いました。
今回はこのローパスフィルタについて、伝達関数を用いてプログラムに直す作業をやってみたいと思います。
制御工学(伝達関数)の力を借りて、LPFをプログラムにする
ローパスフィルタは伝達関数で表現すると以下のようになります。
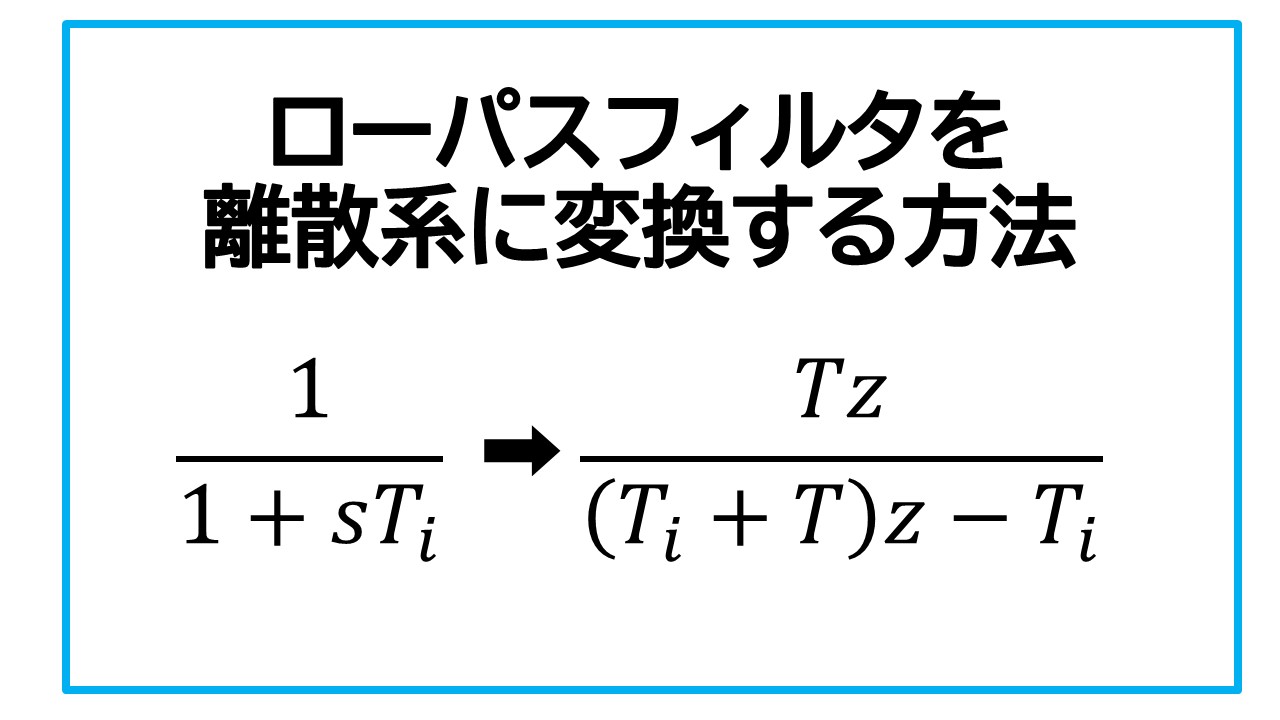
$G(s)=\dfrac{1}{1+sT_i}$
なんでこれがローパスフィルタの式なのか、ということはRC直列回路の伝達関数を導出するととてもわかりやすいのですが、これはググレカス案件なので特に解説はしません。(わかりやすいサイトがいっぱいあります。)
この式はアナログ値を扱うものですが、連続的な量を扱うアナログ回路などのシステムではそのまま使えます。
ですがマイコン等の「サンプリング周期ごとに何かの処理を実行する」ようなシステムにおいては、そのまま使えません。
なのでマイコンのプログラムで使える式に形を直す必要があります。
以降はこの作業を、つまり離散時間(デジタル)系に直す、と表現しようと思います。
伝達関数を離散系に直す方法
それでは実際にやっていきます。
連続系(アナログ)の伝達関数を離散系(デジタル)に直す方法ですが、いくつかの手法があります。
なので最初に、「離散系に直す手法」を決定していきます。
今回紹介する手法ですが、簡単に言うと連続系の式をいろいろ代入して式変形するだけで離散系になるというものです。
この時代入するものについてですが、いくつかのパターンがあります。
偉大な先人たちが連続時間系と離散系の両方で同じシステムとして成り立つように考えてくれたものが、いくつかある感じ。
なのでそのうちどれを使うかを決めようという話です。
結構マニアックな手法も探せばあるみたいですが、一般的に使われたり教科書に載っていたりするのは以下の方法です。
- インパルス不変方式
- 後退差分方式
- 双一次変換
- 整合z変換
どれにもメリット・デメリットがあり、連続系から離散系に変換した場合の応答などが変わってきます。
ですが、その説明は省きます。(ググればたくさん出るしッ俺も完璧に説明できんッ!)
今回はこのうち簡単に変換できる「後退差分方式」を用いることにします。
後退差分を用いてアナログのLPFを離散化(プログラム化)する
後退差分方式を用いて連続系の伝達関数を離散化する場合、以下のような変換式を使います。
$C[z] =C_c(s){|}
s={\dfrac{z-1}{Tz}} $
ん?だから何?、、となりそうですが、別に難しくはないです。
意味は連続系(Continuas)の伝達関数$C_c(s)$に含まれるラプラス変換の$s$を、$\frac{z-1}{Tz}$に置き換える。
ただそれだけです。
やってみましょう。
定義について
と、その前に、いくつか定義についてメモしておこうと思います。
このあたりを明確に意識しておかないと、何が何だかわからなくなるので注意です。
今回の説明においては、以下のように定義します。
連続系→離散系へ変換する1次ローパスフィルタの伝達関数は以下のものとする。
$G(s)=\dfrac{Y[s]}{X[s]}=\dfrac{1}{1+sT_i}$
各変数の意味は以下のように定義する。
・$T_i$はローパスフィルタの時定数とする。
・$X[s]$や$X[z]$は、連続時間系でのX、離散時間系でのXを意味するものとする。
・$T$はサンプリング周期(離散系が動く周期)とする。
・離散時間系において、XやYは現在の値、zがかかったものは未来の値、${z{^-1}}$がかかったものは過去の値を表す。
・$z$の肩にかかっている次数はいくつ先か、過去なのかを表す数である。
結構考えている途中にごっちゃになるので混同しないように意味を把握しておきましょう。
実際に変換してみよう
それでは、実際に連続系のローパスフィルタを離散系へ変換していきましょう。
先ほどの後退差分の変換式を$s$へ代入します。
$\dfrac{Y[s]}{X[s]}=\dfrac{1}{1+sT_i}
\rightarrow
\dfrac{Y[z]}{X[z]}=\dfrac{1}{1+T_i*( \dfrac{z-1}{Tz})}=
\dfrac{Tz}{Tz+zT_i-T_i} $
このようになりました。
次にこれを分母と分子をかけ合わせて一つの式にします。
かけ合わせると以下のようになります。
$TzY+T_izY-T_iY=TzX$
ここで先ほど述べた”z”領域でのルールを再確認しますが、
$z$がないものは現在の値、$z$がかかったものは未来の値、$z^-1$がかかったものは過去の値を表します。
なお、zの肩にかかっている次数は何個先か、何個前の値なのかを意味します。
つまり、上記の式において、
左辺:「$T$×1つ先のY」+「$T_i$×1つ先のY」ー「$T_i$×現在のY」
右辺:「$T$×1つ先のX」
を表しています。
ここまでで変換は半分終了しているのですが、ここで「ん?未来の値ってどこから取得するんだ?」と感じる方は多いと思います。
それはその通りで、現在の計算において未来の値を使うことは原則できません。
なので、この式の両辺に$z^-1$をかけて全体の時間を一つ過去に戻します。
この操作を行うと、上記の式は以下のように変換されます。
$TzY+T_izY-T_iY=TzX$
↓↓↓
$TY+T_iY-T_i{z^{-1}}Y=TX$
以上の操作を行ったことで、
左辺:「$T$×現在のY」+「$T_i$×現在のY」ー「$T_i$×1つ過去のY」
右辺:「$T$×現在のX」
というように、取得可能な値で構成された式に変換されたことが分かるでしょう。
正直このあたりの説明が抜けている教本が多いのでよくわからなくなるんじゃないかなぁ~と、個人的には思いますね。。
さらにこの式を変形して、取得したい現在の$Y=$の形に式変形を行うと、
$TY+T_iY-T_i{z^{-1}}Y=TX$
$(T+T_i)Y=T_i{z^{-1}}Y+TX$
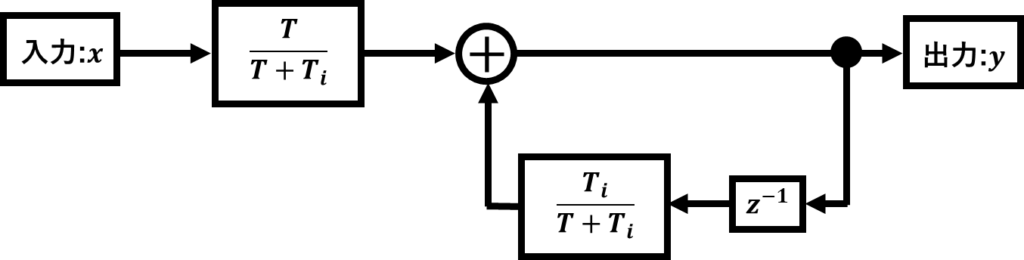
$Y[z]=\dfrac{T_i}{T+T_i}{z^{-1}}Y+\dfrac{T}{T+T_i}X$
となります。
以上で連続系から離散系への変換が終わりました。
この離散系の式をブロック線図に直すと以下のようになります。
プログラムに直してみる
とりあえずここまでで連続系から離散系への変換は終わりました。
ただ実際に使うとなるとプログラムに直す必要があるのでもう少しだけ説明をしようと思います。
プログラムへの対応について
先ほどの式を再掲します。
$Y[z]=\dfrac{T_i}{T+T_i}{z^{-1}}Y+\dfrac{T}{T+T_i}X$
この式に含まれる値は全て取得可能な値になっています。
固定の変数であるサンプリング周期$T$とLPFの時定数$T_i$は定数で設定してやれば問題ありません。
${z^{-1}}Y$は一見どう書くのか迷いますが、これは先ほど説明した通り、一つ前の出力結果である$Y[n-1]$を表します。
なので変数等で一つ前の値を保存しておけば問題ありません。
※プログラム的な表現では、$Y[n]$を現在の値、$Y[n-1]$を一つ前の値、$Y[n-x]$をx個前の値とすることが多いようです。
プログラム
それでは実際にプログラムを作成していきます。
先ほどの式をプログラム的に直すと(zをプログラム的な解釈に変換すると)、
$Y[n]=\dfrac{T_i}{T+T_i}Y[n-1]+\dfrac{T}{T+T_i}X[n]$
のようになります。
ブロック線図としては以下のようになります。
これを先ほどのブロック線図に適用すると、意味合いとしては以下のようになります。
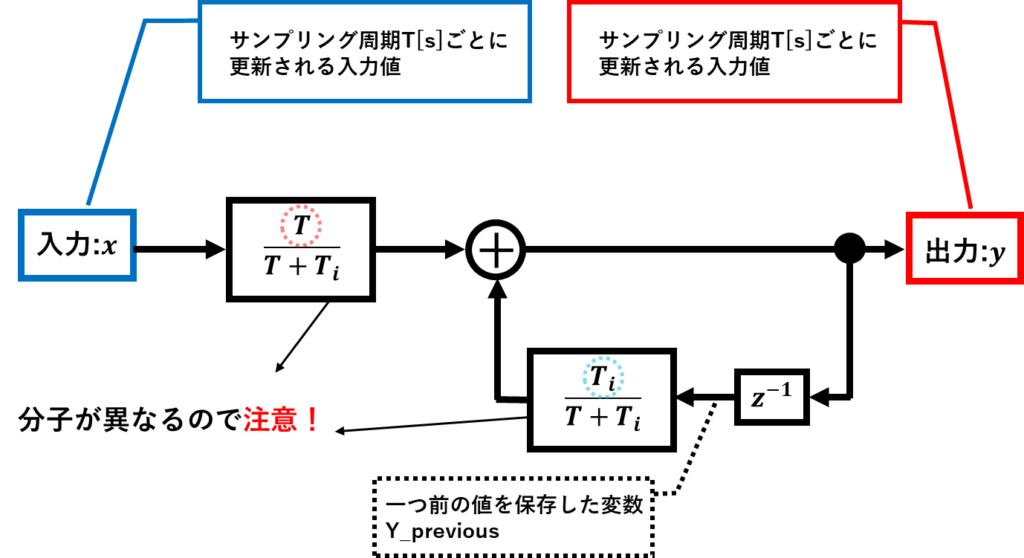
C++を例として、これをプログラムに起こすと以下のようになります。
#include <math.h>
float T=T_sample; //マイコンのサンプリング周期[s]です。割り込み周期等と一致させてください。
const float Ti=0.5; //LPFの出力が入力値の63.2%に到達するまでの時間です。
static float X=0; //入力値を代入する変数
static float Y=0; //出力用の変数
static float Y_prev=0; //前回の出力を保存するための変数。※static宣言で上書き防止してください
void loop(){ //マイコン起動後に繰り返される部分
X=sensor_output;
Y=Ti/(T+Ti)*Y_prev+T/(T+Ti)*X; //離散系でのLPFの演算
Y_prev=Y; //今回の出力を次回使うために値を保存する。
}サンプリング周期ごとに更新される、センサからの取得値であるXと、保存した前回の出力値であるYをもとに計算を行います。
応答を確認する
それでは、上記のプログラムを用いて実際の応答を確認してみます。
シミュレーションソフトにはPLECSを用いました。連続系のシミュレーションとの比較も行ってみます。
時定数Tiが設定値通りか確認する
設計したフィルタの時定数は0.5秒としました。
シミュレーションの条件は分かりやすいように、
- サンプリング周波数:20,000[Hz]
- LPFの時定数:0.5[s]
- 入力値、1.0
としました。
シミュレーション結果は以下のようになりました。
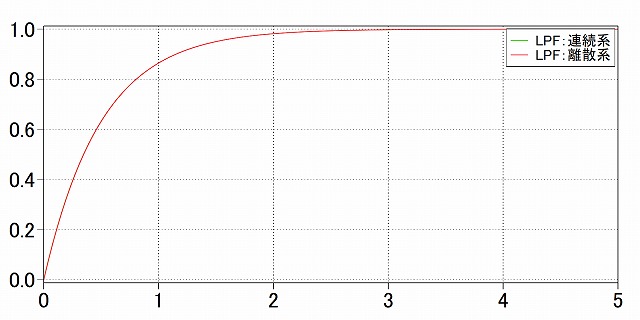
まず見た目で連続系と離散系が一致していることが確認できます。
次にカーソルを使ってLPFの出力が0.5[s]経過時に63.2%に到達しているか確認します。
※一般に、step入力指令値の63.2%に到達するまでの時間が、その系の時定数になります。
結果は以下のようになりました。
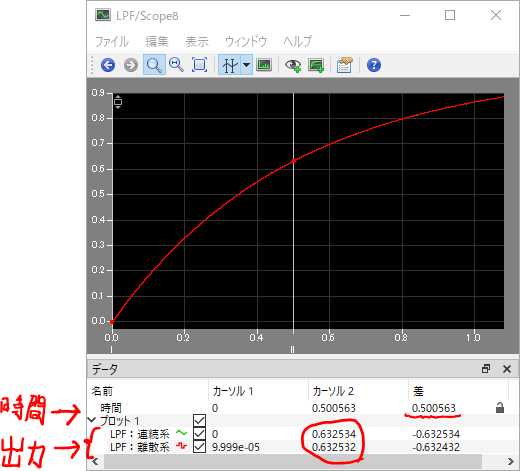
時定数が設計通り、0.5[s]になっていることが確認できますね。
以上のことから、
以上で連続時間系のLPFを離散系に変換し、正しくプログラムに直すことができました。
まとめ
以上、連続時間系のローパスフィルタをz変換を用いて離散時間系に直し、プログラムに起こす方法について確認しました。
結構段階を踏んで解説したので割と理解しやすいのではないかと思います。
今回は後退差分を用いましたが、双一次変換等、もう少し性能がいい変換方式や異なる特徴を持つように変換する方法も存在します。
ただあまり厳しい使い方をしないのならば、今回の方法でも十分実用に足りうるとは思います。
今回は手軽に使える方法について解説してみました。
お役に立てれば幸いです。