どうも初めまして、アイスメガネです。
最小公倍数なんてネットの計算サイトつかえばいいじゃぁ~んんんんぬううう
って思うんだけどこういう課題出るんだよねぇ、、、
今回は3つの数の最小公倍数を求めるプログラムを考える、そういう内容です。
最小公倍数を求める方法について(ユークリッドの互除法)
最小公倍数を求める方法には「ユークリッドの互除法」というものがあるみたいです。
手順としては、
①最大公約数をもとめる
②二つの数の積を最大公約数で割ることで最小公倍数が求まる。
ということらしいです。
さっそく説明に入ります。
①最大公約数をもとめる
例として適当に1534と1390を使います。
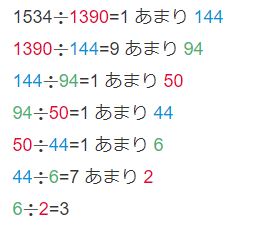
以下のような計算でどんどん割っていきます。色を分けましたが、次に段に移った時に数字がシフトします。以下で説明します。
1534$\div$1390=1 あまり 144
1390$\div$144=9 あまり 94
144$\div$94=1 あまり 50
94$\div$50=1 あまり 44
50$\div$44=1 あまり 6
44$\div$6=7 あまり 2
6$\div$2=3
このような感じで計算を進め、あまりが0になるまで割り続けます。
よって最大公約数は$2$ということになります。
ちょっと例に挙げたのが計算長いうえに簡単な答えなので例が少し悪ですね、、、
他の数でもできるので確認したい人はやってみてください。
計算の文字の移り方ですが、左側の数が分子、右側の数が分母ということを頭に入れて見てみると、
一つ目の分母を次の分子にして、あまりを分母にする、という感じに順次シフトして計算します。
これであまりが0になるまで繰り返し計算するのがユークリッドの互除法、というらしいです。
まず①の方法により、最大公約数が求まりました。
②最小公倍数をもとめる
つぎに②の方法により、最小公倍数を求めます。
最小公倍数の式は、
$$最小公倍数 = \frac{数1 \times 数2}{最大公約数}$$
なので、
$$最小公倍数 = \frac{1534 \times 1390}{2}=1066130$$
となります。
数が汚すぎる、、、まじでもっといい数字選べばよかったと思います。。。
とまぁ、こんな感じで求まりました。
これが筆算でやる場合の方法ですね。
プログラムで解く方法を考える
注意:ブログ主はプログラミング経験2か月未満の超初心者です。
きれいなプログラムとかを求める人はこの時点でブラウザバックをお願いします。
問題はここよなぁ、、
筆算なら容易に理解はできるんですが、プログラムに直すとなると、話は変わってきますね。
上のシフトする数ように全部の変数用意する、みたいなおかしなことやらん限りは多少頭を使わないといけません。
プログラムを使う以上、あらゆる入力に対応できないとプログラムにする意味がなくなってしまうのでその辺も少し考えないといけません。
こと、私のようなプログラミング初心者となると、ちょっと難易度上がりますねぇ、、、
加えて今回は、「3つの数の最小公倍数を求める」という問題なので、ちょっと特殊です。
二つならできるのになぁ、、、
と思ったんですが、
2つ以上の最小公倍数を求める際は大きい方の数二つを選んでその中で最小公倍数を求め、その最小公倍数とその他の数の内一つ小さい数を用いてまた最小公倍数を計算すればいいらしいです。
日本語だとめちゃめちゃわかりにくいので例えを出すと、
1678、2938、3842の最小公倍数を求めよ、って言われたら、まず2938と3842の最小公倍数を求め、その後にその最小公倍数と1678の最小公倍数を求めればいいってことらしいです。
これシンプルに考えればわかる話なんですけど、意外に見落としていてだいぶ時間をロスしてしまいました。
あと、これ、ネットにあんまり載ってなかったです。単純すぎるからかな。
それが一番つらかった。
具体的なプログラム
それではプログラムに入りたいと思います。
言語はC++を、実行はVisualStudioのコンソールアプリで行いました。
小分けにすると逆にわかりにくくなると思うので、まず最初にプログラム全部を載せます。
環境によっては「scanf」を「scanf_s」にしないと動かないかもしれませんが、
それ以外は基本的にコピペで動作すると思います。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void input();
void sort();
void verif();
int remain(int x1, int x2);
void lcm_calc(int sn1, int sn2, int sn3);
int array[10];
int nn_number = 3;
void main()
{
int sn1, sn2, sn3;
int i, j, box, ii;
int lcm1;
puts("3つの数を入力してください。");
printf("\n");
input();
sort();
sn1 = array[1]; sn2 = array[2]; sn3 = array[3];
lcm_calc(sn1, sn2, sn3);
}
void input() {
int i;
for (i = 1; i <= nn_number; i++)
{
printf("自然数%d:n%d = ", i, i); scanf("%d", &array[i]);
}
printf("\n");
}
void sort() {
int i, j, box;
for (i = 1; i <= nn_number - 1; i++)
{
for (j = i + 1; j <= nn_number; j++) {
if (array[i] < array[j]) {
box = array[i];
array[i] = array[j];
array[j] = box;
}
}
}
}
int remain(int x1, int x2) {
int quo, remainder;
quo = x1 / x2;
remainder = x1 - quo * x2;
return remainder;
}
void lcm_calc(int sn1, int sn2, int sn3) {
int i, flag1, seki, lcm;
for (i = 1; i <= 2; i++) {
if (i == 2) {
sn1 = lcm;
sn2 = sn3;
}
flag1 = remain(sn1,sn2);
seki = sn1 * sn2; //順序
while (flag1 != 0)
{
sn1 = sn2;
sn2 = flag1;
flag1 = remain(sn1, sn2);
}
lcm = seki / sn2;
}
printf("最小公倍数:lcm = %d\n", lcm);
return 0;
}とりあえずこんな感じになりました。
初心者なのでかなり雑です。
細かいところは以下のような感じです。
void main() の部分
void main()
{
int sn1, sn2, sn3;
int i, j, box, ii;
int lcm1;
puts("3つの数を入力してください。");
printf("\n");
input();
sort();
sn1 = array[1]; sn2 = array[2]; sn3 = array[3];
lcm_calc(sn1, sn2, sn3);
}main()はこんな感じです。
うえから順に
putsで文字列を出力、改行
input(),sort()の二つの関数で入力文字を配列に格納、大きい順に並び替えを行っています。
sn1,sn2,sn3の三つ整数型変数を用意し、それぞれ配列に代入した数を代入しています。
ぶっちゃけこの処理いらんかったな、、、
次にlcm_calcで三つの数字を引数として入力し、
その結果を出力してます。
結果は関数内で出力させました。
void input() の部分
void input() {
int i;
for (i = 1; i <= nn_number; i++)
{
printf("数%d:n%d = ", i, i); scanf("%d", &array[i]);
}
printf("\n");
}ここに関しては述べるまでもないですが、Forループでnn_number(比較に用いる自然数の数。)まで、つまり1から3まで回すことを指定しています。printf関数に実引数二つを渡してn番目も自動でかわるようにしてあります。残念ながらまだnコの数には対応させられていませんが。
これでarray[1]~array[3]に三つの数字が入力されます。array[0]を使うと、1の時0、2の時3、のようになって面倒なので飛ばしました。
void sort() の部分
void sort() {
int i, j, box;
for (i = 1; i <= nn_number - 1; i++)
{
for (j = i + 1; j <= nn_number; j++) {
if (array[i] < array[j]) {
box = array[i];
array[i] = array[j];
array[j] = box;
}
}
}
}このような感じです。
単なるバブルソートになります。順に追っていくと、
まず外側のループは1から2まで回ります。
内側のループは2から3まで回ります。
内側のループが回りきると、外のループのjが動いて今度は2になり、
内側のループは3から回り始める、といった感じになってます。
今回は比較する数が3つしかないのであんまり訳に立たないですね。
ソーティングアルゴリズムはバブルソートやクイックソート、などで検索すればたくさんでてくるので詳しく説明しません。
remain() の部分
int remain(int x1, int x2) {
int quo, remainder;
quo = x1 / x2;
remainder = x1 - quo * x2;
return remainder;
}ここの関数はA % Bを計算する(二つの数を割った余りを出す)プログラムです。返り値としてremainderが指定されているのであまりの数が返されます。
lcm_calc
void lcm_calc(int sn1, int sn2, int sn3) {
int i, flag1, seki, lcm;
for (i = 1; i <= 2; i++) {
if (i == 2) {
sn1 = lcm;
sn2 = sn3;
}
flag1 = remain(sn1,sn2);
seki = sn1 * sn2; //順序
while (flag1 != 0)
{
sn1 = sn2;
sn2 = flag1;
flag1 = remain(sn1, sn2);
}
lcm = seki / sn2;
}
printf("最小公倍数:lcm = %d\n", lcm);
return 0;
}順にみていきます。
まずsn1,sn2,sn3から引数として呼び込んだ3つの数が入ってきます。
この時sn1,sn2,sn3はソートされているので、sn1が一番大きく、sn3が一番小さいです。
そして最初のループに入ります。この時i=1です。
最初のif文はi = 2の時なので特に働きません。
そのまま下に行き、今度はflag1が計算されます。
remain(sn1,sn2)なので、大きい方の数を小さい方の数で割った数のあまりが出ます。
つぎにsekiという変数に、大きい方の数と小さい方の数をかけた数が代入されます。
この処理は上で示した↓この処理の分子にあたります。
$$最小公倍数 = \frac{数1 \times 数2}{最大公約数}$$
次にWhileループに入ります。この中ではflag1、という変数が0ではなくなるまで動作します。このflag1ですが、上で述べたように二つの数を割った余りです。
つまり、上記で示した↓この最後の部分まで動く、ということです。(余りがなくなるまで動きます。)

なかの式を見てみます。
while (flag1 != 0)
{
sn1 = sn2;
sn2 = flag1;
flag1 = remain(sn1, sn2);
}まず、flag1が0出なかったら、つまり大きい方の数が小さい方の数で割り切れなかった場合、
sn1にsn2が代入されます。
今、sn1は大きい方の数なので、分子に来る数です。sn2は小さい方の数なので分母に来た数です。
つまりここの代入は、上記のユークリッドの互除法に基づき、一度目で割り切れなかたので、最初に分母に来ていた数を分子に持ってきたということをしている処理になります。
次にsn2にflag1を入れます。
これはsn2つまり分母(割る数)に上記画像において一行上の計算ででたあまりを代入している処理でになります。
これで二行目に移ったことになります。
ここで再びflag1という関数を定義し、remain(A,B)をつかってA$\div$Bhのあまり、つまり大きい方の数を上段の余りで割った数のあまりを求めます。(二つの数の余りを求め、flag1に代入します。)
この時点で、一行目の計算で求めたflag1、つまり一行目のあまりのデータは消えますが、もう使わないので問題ないです。
代わりに2行目の余りが残ります。
ここでもflag1が0とならなかった場合、まだWhileループを抜けることはできないので、もう一度
ループ内で計算が行われます。
そして今度は今まで説明した流れを3行目で行い、繰り返す、というわけです。
これで割り切れた場合、その時に分母に来ている数が最大公約数なので、Whileループを出たときのsn2が最終的に求まった最大公約数というわけです。
そして、ユークリッドの互除法は比較対象の二つの数をかけた数を最大公約数で割ることで求まる、というものなので、
lcm = seki / sn2; よりlcm(最小公倍数)が求まります。
そしてここまで来て i = 1 の場合のForループが終了します。
そして次はi=2の場合に入ります。
ですが特に難しいことはなくまずこの部分で代入が行われます。
if (i == 2) {
sn1 = lcm;
sn2 = sn3;
}これにより、sn1(最初に分母に来る数)がlcmに置き換えられます。そしてsn2(最初に分子に来る数)にsn3(比較対象とした三つの数の中で最も小さかった数)が代入されます。
なぜこれができるかというと、最初に説明したように、ユークリッドの互除法において、
複数の数の内大きい方の数二つで最小公倍数を求めてから、その最小公倍数とそれらより一つ小さい数の二つでもう一度最小公倍数を計算することで複数の数全体の中での最小公倍数が求まるからです。
つまりもうsn1とsn2そのものデータはいらない、からですね。
あとは今までながながと説明してきた流れをこの二つの数で繰り返していくだけです。
まとめ
アルゴリズムって今回みたいな簡単なものでも動くとものすごい感動するなぁ~と思います。
個人的にはsn1とsn2を上書きしていいっていうのを思いつくのに時間がかかった。
アルゴリズム的な考え方?みたいなものをパッと思いつくようになるにはもっと数こなさないといけないんだろうなぁ、、とつくづく思います。
次は$n$個の数の最小公倍数を求めるプログラムを作ってみようかな。
それでは。