どうも、バイト戦士です。
今回はモータの回転時などに生じる誘導起電力の一つである「変圧器起電力」を導出してみました。
変圧器起電力に関する概要
変圧器起電力とは?
変圧器起電力とは、コイルに鎖交する磁束の磁束密度$B$が時間的に変化した場合に発生する起電力のことです。
磁束を中心に考えるファラデーの法則で導くことができます。
フレミングの法則から導くことはできません。
変圧器起電力?誘導起電力や速度起電力との違いは?
「起電力」という言葉が付く単語は結構な数がありますが、厳密には同じものを指しているわけではありません。
よく見かける誘導起電力や速度起電力との関係をまとめてみると以下のような感じです。
誘導起電力=速度起電力+変圧器起電力
教科書などでよく出てくる誘導起電力とは、速度起電力と変圧器起電力を合わせたものになります。
フレミングの右手の法則とファラデーの法則(導出準備)
実際に変圧器起電力とはどんなものなのかを導出してみたいと思います。
導出に用いるのはファラデーの法則とフレミングの右手の法則です。
まずは二つの法則の概要を示してみます。
フレミングの右手の法則
フレミングの法則は右手の法則と左手の法則の二つがあります。
左手の法則は、電流$i$と磁界(磁束密度$B$)によって力$f$が発生するというものです。式は以下となります。
$$f=i \times B \times l [N]\hspace{30cm}$$
左手の法則は中学校でもの習うのでより有名だと思います。
右手の法則は、「磁界と運動(速度)$v$から起電力$e$が発生する」というものです。式は以下となります。
$$e=v \times B \times l [V]\hspace{30cm}$$
磁界や電流、物体の速度から簡単に起電力の大きさなどを求められる便利な式です。
誘導電流が流れる向きは誘導起電力が発生する向きと同じなので、右ネジの法則を合わせて使えば発生する起電力の向きもわかります。
ファラデーの法則とは?
ファラデーの法則とは、「回路に誘導される起電力は回路に鎖交する磁束の時間変化に比例する」という法則です。
式で表すと、次のようになります。
$$e=-N\frac{dφ}{dt}\hspace{30cm}$$
ここで、
・$N$:巻き数
・$φ$:磁束
・$e$:誘導起電力
・$Ψ$:鎖交磁束
です。
導出の流れ
今回は「変圧器起電力」を導出するわけですが、いきなりは導出しません。
まずは一般的な概念である「誘導起電力」を導出します。
誘導起電力は”フレミングの右手の法則”と”ファラデーの法則”のどちらでも導出できますが、コイルに鎖交する磁束が一定ではない(時間的に変化した場合)、結果が異なります。
これは変圧器起電力がファラデーの法則でしか導出できないためです。
「誘導起電力」という大きい概念を2つの法則で求めてから、生じた違いについて「これは速度起電力」「これは変圧器起電力」といった感じに説明した方がやりやすいので、
フレミングの右手の法則で誘導起電力を導出
↓
ファラデーの法則で誘導起電力を導出
↓
磁束を中心に考えるファラデーの法則で違いが出た
↓
これが変圧器起電力
という流れにします。
ファラデーの法則だけでまとめてもいいですが、それだと磁束密度が時間変化したときのみ変圧器起電力が現れる、ということを示しにくいので、フレミングの右手の法則も用いて説明を行ってみます。
(逆にややこしく感じる人がういたらスマンヌ。)
フレミングの右手の法則から誘導起電力$e$を求めてみる
まずはフレミングの右手の法則から誘導起電力を求めてみます。
導出には一回巻コイルを用いたモーターで考えます。
※ちょっとややこしい(ここは読まなくてもいいです)
モータは磁界の中にある導体に電流を流して発生した力 $f$を用いて回転しているので、回転原理としてはフレミングの左手の法則です。ですがそのとき、磁界中で導体が動いているという事実が存在するため、「モータはフレミングの左手の法則で回転し、その時のコイルにはフレミングの右手の法則による起電力が生じている」という状態になります。
モータの回転原理を用いて説明しているのではなく、回転しているモータのコイルの状態を用いて説明している点に少し注意が必要です。
まず導体が動く速度vを求める
フレミングの右手の法則は、
$$e=v \times B \times l [V]\hspace{30cm}$$
です。磁束密度$B$と導体の長さ$I$は直流モータでは一定値ですが、速度$v$は時間によって変化します。
そのためまずは速度$v$を求めます。
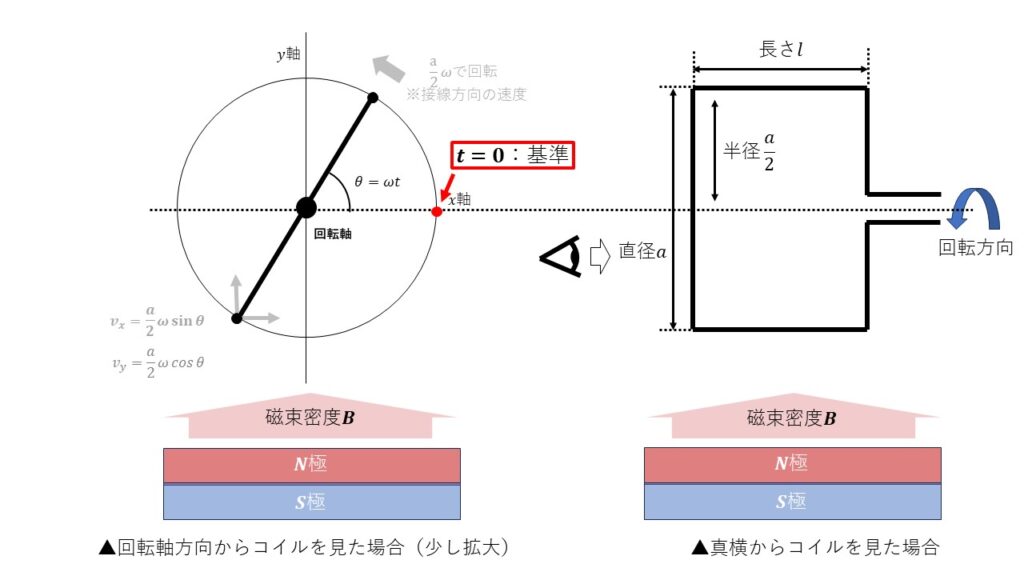
直径が$a$のコイルを考えた場合、モータが一定の速度で回転しているときの接線方向の速度は以下の図のように考えることができます。

ここで速度は$v_x$のみ使用します。理由は起電力$e$に寄与するのは磁界を横切るように動く成分のみだからです。
これを踏まえてコイルを回転軸方向からみた場合、導体(コイルの端の2辺)が磁束密度Bの磁界中を動く速度は以下の式で表されます。
$$v= \frac{a}{2} \omega sin \theta = \frac{a}{2} \omega sin( \omega t)\hspace{30cm}$$
基本的には、単振動と同じ考え方で導くことができます。
※磁束密度Bの磁界と運動の方向が直行した瞬間が最も速くなります。($\theta=90°, 270°$)
※磁束密度Bの磁界と運動の方向が直行しない瞬間が最も遅くなり、速度0となります。($\theta=0°, 180°$)
誘導起電力$e$を導出する
次に求めた速度$v$を用いて、フレミングの右手の法則からコイルに発生する力 $f$を導出します。
この後時刻$t$を用いて計算を進めますが、基準点はコイルの移動方向と磁界の方向が平行になった時、つまりコイルに力が発生していないときを$t=0$として考えます。
まずフレミングの右手の法則に先ほど導出した速度$v$を代入します。
$$e=vBl\hspace{30cm}$$
$$=\left( \frac{a}{2} \omega sin(\omega t) \right) \times Bl\hspace{30cm}$$
これがコイルに発生している誘導起電力になります。しかしこれでは少し間違いです。
今回考えているコイルは単なる導体棒ではなく1回巻のコイルです。そのため上の辺としたの辺でそれぞれ誘導起電力が発生します。
上の導体と下の導体は一つのコイルなので直列接続されていることになります。
よって起電力も単純に足し算して、以下の式で表すことができます。
$$e=2\times \left(\frac{a}{2} \omega sin(\omega t)\right) \times Bl\hspace{30cm}$$
$$e=Bal \omega sin(\omega t) \hspace{30cm}$$
これが磁界中を動く1回巻コイルに発生している誘導起電力になります。
ファラデーの法則から誘導起電力$e$を求めてみる
次にファラデーの法則から誘導起電力$e$を求めます。
今回も導出には1回巻コイルを用いたモータで考えます。
まず鎖交磁束$φ$を求める
ファラデーの法則は最初に示した通り以下の式です。
$$e=-N\frac{dφ}{dt}\hspace{30cm}$$
Nは巻き数で固定値ですが、鎖交磁束$φ$は時間によって変化します。
そのためまずは鎖交磁束$φ$を考える必要があります。
鎖交磁束とは、コイルを貫く磁束の有効分を表します。鎖交磁束(磁束)$φ$と磁束密度$B$、鎖交する面積$S$の関係は以下の式で表すことができます。
$$φ=BS\hspace{30cm}$$
モータの磁石に永久磁石を使用している場合、磁束密度$B$は一定なので変化せず、磁束が通る面積$S$(コイルの内側に通る面積)だけが変化します。
図にしてみると以下のようになります。

フレミングの法則を使ったときと同じく時間$t$の基準をそろえるとして、先ほど示した鎖交磁束を求める式に代入すると、回転する一回巻コイルに鎖交する磁束は以下のように求めることができます。
$$φ=B(S)\hspace{30cm}$$
$$=B \times (a\times l \times cos(\omega t))\hspace{30cm}$$
$$=alBcos(\omega t)\hspace{30cm}$$
以上が一回巻コイルに鎖交する磁束になります。
※$\theta=0^{\circ}$の時に面積$S$は最大となります。→$cos(\omega t)$において$t=0$で$cos(0)=1$
※$\theta= 90^{\circ} $の時に面積$S$は最小になります。
誘導起電力$e$を導出する
ファラデーの法則に戻ります。先ほど求めた鎖交磁束の式と1回巻コイルのN=1を代入すると、以下のようになります。
$$e=- \frac{dφ}{dt}\hspace{30cm}$$
$$- \frac{d( Bal cos(\omega t)) )}{dt} \hspace{30cm}$$
これを積分すれば、
$$e=Bal \omega sin(\omega t)\hspace{30cm}$$
となります。
これが磁界中を動く1回巻コイルに発生している誘導起電力になります。
フレミングの右手の法則を用いて導出した場合と全く同じになっています。
変圧器起電力を求めていく
ここまでで「磁束密度$B$が一定であれば」発生する誘導起電力に違いがないという結果がわかりました。
次は磁束密度$B$が時間的に変化したらどのように変わるのか、同じ手順を踏んでみていくことにします。
※この記事の冒頭で、導出の流れを以下のように行うと述べました。
フレミングの右手の法則で誘導起電力を導出
↓
ファラデーの法則でで誘導起電力
↓
差が生じた
↓
変圧器起電力
次はタイトルの「変圧器起電力」を求めていきます。
最初に述べた通り、変圧器起電力とはコイルに鎖交する磁束の磁束密度$B$が時間的に変化した場合に発生する起電力のことです。
つまり磁束密度自体が時間の変数でなければいけません。
よって導出のために磁束密度$B$(磁界)を時間で変化する関数として、以下の式でおいてみます。
$$B=B sin(t)\hspace{30cm}$$
フレミングの右手の法則を用いる場合
まずはフレミングの法則に時間変化する磁束密度$B$を代入してみます。
フレミングの法則は以下の式となります。
$$e=vBl\hspace{30cm}$$
これまでに導出したように、$v$、$B$、$l$を単純に代入して、
$$e=2\times{\frac{a}{2} \omega sin(\omega t)}\times{Bsin(t)}\times{l}\hspace{30cm}$$
$$=alB\omega sin(t)sin(\omega t)\hspace{30cm}$$
となります。
ファラデーの法則を用いる場合
次にファラデーの法則でも同じように代入してみます。
鎖交磁束$φ$は、$φ=BS$で求まるので、
$$φ=Bsin(t)\times alcos(\omega t)\hspace{30cm}$$
となります。
この式は、回転によって変化する鎖交面積$S$と時間変化する磁束密度$B$の2つの要因で鎖交磁束が変化していることを表しています。
次にファラデーの法則に代入して起電力$e$を求めてみます。
上記の式において、磁束密度$B$と面積$S$はともに時間$t$の関数であるため、積の微分公式を用いて解くことになります。
よって、
$$e=-\frac{dφ}{dt}\hspace{30cm}$$
$$ =-1\times \frac{d\{ Bsin(t)\times alcos(\omega t) \}}{dt} \hspace{30cm}$$
$$=-1\times \{ (Bsin(t))' alcos(\omega t) +Bsin(t) (alcos(\omega t))' \}\hspace{30cm}$$
$$=alB \omega sin(t)sin(\omega t) - alBcos(t)cos(\omega t)\hspace{30cm}$$
となります。
2つの式を比較する
ここで、磁束密度$B$が時間変化した場合の誘導起電力の式2つを比較してみます。
フレミングの法則:$e=alB \omega sin(t) sin(\omega t)$
ファラデーの法則:$e=alB \omega sin(t) sin(\omega t)- alB cos(t) cos(\omega t)$
上記のようになりました。
フレミングの法則、ファラデーの法則はともに「誘導起電力」を求めることができる式です。
ですが磁束密度$B$が時間的に変化すると仮定した場合、磁束を中心に考えるファラデーの法則での結果で1つ項が増えました。
これがコイルに鎖交する磁束の磁束密度$B$が時間的に変化した場合に発生する変圧器起電力になります。
また共通の項もありますが、これは「速度起電力」とよばれます。
導出のまとめ
冒頭部分でも述べましたが、改めてまとめておきます。
変圧器起電力とは?
変圧器起電力とは、コイルに鎖交する磁束の磁束密度$B$が時間的に変化した場合に発生する起電力のことです。
磁束を中心に考えるファラデーの法則で導くことができます。
フレミングの法則から導くことはできません。
変圧器起電力?誘導起電力や速度起電力との違いは?
「起電力」という言葉が付く単語は結構な数がありますが、厳密には同じものを指しているわけではありません。
よく見かける誘導起電力や速度起電力との関係をまとめてみると以下のような感じです。
誘導起電力=速度起電力+変圧器起電力
教科書などでよく出てくる誘導起電力とは、速度起電力と変圧器起電力を合わせたものになります
まとめ
今回は1回巻のコイルを用いたモータを例に、変圧器起電力を導出してみました。
小中高での教科書で電磁誘導や誘導起電力について語られる場合、磁石は永久磁石でローター側が巻線のDCモータを用いることがほとんどだと思います。(ステータの磁束分布は時間によらず一定)
このようなモータでは「変圧器機器」は発生しないので、一般的な「誘導起電力」≒「速度起電力」というイメージもあながち間違ってはいないのかなと感じます。
それでは、また。
