配列の要素の並びを逆転させるプログラム。
配列のを引数として渡すやり方の復習と計算方法も兼ねて。
コード全体
#include <iostream>
void change_array(int v[], int n) {
int i, n_count;
int box;
n_count = n / 2; //例えばn=7なら、7/2=3.5だが、n_countは整数型なので、=3となる。
for (i = 0; i < n_count; i++) { //nが3未満、すなわち2まで実行されれば、三回交換される。
box = v[i];
v[i] = v[n - i - 1];
v[n - i - 1] = box;
}
}
void print_array(const int v[], int n) {
int i;
printf("{");
for (i = 0; i < n; i++) {
printf("%3d", v[i]);
}
printf("}\n");
}
int main()
{
int min = 0;
int tensu[] = {1,2,3,4,5,6};
int number = 6;
print_array(tensu, number);
printf("配列内の並びを逆転した配列は以下の通りです。\n");
change_array(tensu, number);
print_array(tensu, number);
}意味
簡単に意味をメモ。
文中にもあるが、配列の中身を並び替える場合は、要素数全部を並び替えるのだが、
「交換する」という手法でやる場合、お互いに対極に位置する数を交換することになる。
ただここで注意すべきことが一つある。
{ 1 , 2 , 3 , 4 , 5 }
のように奇数個の要素数の場合は3を中心に交換が行われる。
しかし、
{ 1 , 2 , 3 , 4 , 5 , 6 }
のように要素数が偶数個の場合は、中心はない。
この点に注意すると以下のようなプログラムになる。
void change_array(int v[], int n) {
int i, n_count;
int box;
n_count = n / 2; //例えばn=7なら、7/2=3.5だが、n_countは整数型なので、=3となる。
for (i = 0; i < n_count; i++) { //nが3未満、すなわち2まで実行されれば、三回交換される。
box = v[i];
v[i] = v[n - i - 1];
v[n - i - 1] = box;
}
}要素数をnとして読み込んだわけだが、例えば要素数がn=7だった場合は、
1-7、2-6、3-5を交換し、4が中心になる。
配列の要素番号で言えば、それぞれからマイナス1して、
0-6、1-5、2-4、3中心、となる。
つまり、交換する回数は要素数÷2したときの整数部分、となる。
1回なら0回
2回なら1回
3回なら1回
4回なら2回
5回なら2回
6回なら3回
7回なら3回
これより、n / 2 で交換回数が求まるわけなのだが、これでは3.5とかになる、と思うかもしれないが、
nはint型で宣言しているので、割り切れるうちの整数分が残るのである。
これで「n_count = n / 2」の意味が分かるだろう。
注意点
配列の要素を入れ替える際に注意すべき点が一つある。
for (i = 0; i < n_count; i++) {
box = v[i];
v[i] = v[n - i - 1];
v[n - i - 1] = box;
}それはこの部分である。
入れ替える際や回数は「i< n_count」としているので未満、なって配列の要素と合うのだが、
交換する際はnと配列の要素が合わないので注意。
v[n]という配列は存在しない。
ちなみにミスすると以下のようなエラーが出る。
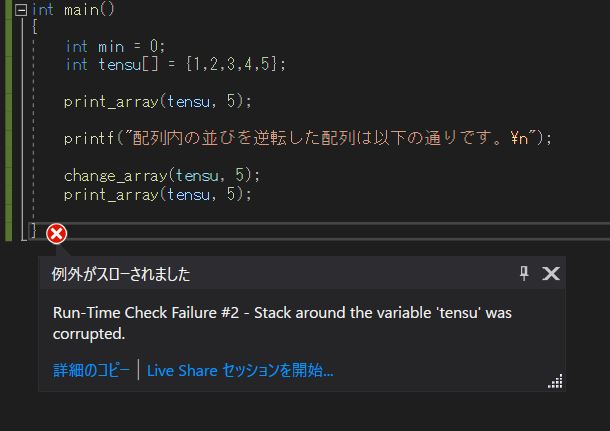
「配列の要素数がオーバーしてます。」
とか書いてくれればわかりやすいんだけどね。。。。
まぁエラー箇所が分かるだけ感謝。
まとめ
特になし。
配列と要素を用いた計算の場合はwhile文よりfor文のほうがあっているのかなぁ~と思った。
